A Brief Intro

The last post gave a practical example of hex editing. In the post before that I talked about bytes and hexadecimal numbers. This post continues that discussion of theory.

With regard to hexadecimal numbers, its important to note that you don’t need to be able to convert between hexadecimal and decimal in your head, or even on paper, using a calculator for the conversion is fine. All that’s important is to know that the same number can be written both as a decimal and as a hexadecimal. For example if I had a byte in my file which has the value AB, as a decimal this is 171. You may sometimes see numbers prefixed with 0x like 0xAB, this is simply standard notation for a hexadecimal number.

While being able to store a value up to 255 in a byte is useful, being able to store larger numbers is more useful. In this post, I shall discuss some basic types.

Signed and Unsigned Numbers

In mathematics, numbers can be either positive or negative. In computing, sometimes we’ll want numbers that can be either positive or negative, or sometimes we know that a number will always only ever be positive. Why differentiate the two you might ask? Storing whether a number is positive or negative takes up a small amount of data (specifically one bit). If all numbers were treated this way, we would be able to hold a smaller range of data even if we knew that data would never be negative, which while a small limitation is still wasteful.

Signed numbers are numbers which can be considered to have a positive/negative sign information. Supporting negative  numbers comes at the expense of a smaller range of numbers that can be represented.

Unsigned numbers are numbers which must be of the same sign (typically positive). These numbers can support a larger range but at the cost of not being able to store both positive and negative values.

Integers

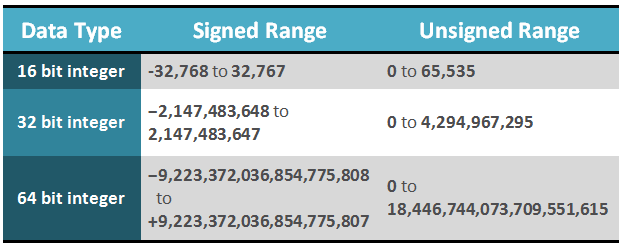
Integers are one of the most basic and ubiquitous data types in computing. They represent whole numbers such as 1, 5, 98 and cannot store fractional numbers such as 0.24, 1.7, 5.5. Integers can be signed or unsigned and come in various sizes. The most common sizes of ints are 16 bit, 32 bit and 64 bit. The number of bits refers to the size that the integer occupies, there are 8 bits to a byte and therefore a 16 bit integer is 2 bytes and a 32 bit integer is 4 bytes. By combining bytes together we extend the range of the data type significantly, the more bytes there are the more variations that can be stored. In the table below I show the range of the above three types of ints as both signed and unsigned numbers.

Little/Big Endian

When it came to writing say the number 123 as a hexadecimal byte, it was quite straight forward. We just worked out it was 7B using the calculator and that was it. If we now take the number 1234 which is bigger than the maximum value a byte can hold (255), we clearly now need to use an integer. So lets take a 32 bit integer which consists of four bytes. So if you put 1234 into your calculator and convert to hex you’ll get the result 4D2. If we stick some zeroes in front of it to occupy four bytes we would then get 00 00 04 D2. That’s great and this is a viable way of writing an integer however its not the only way.

Big endian means that the high numbers come first and the low numbers come last. For example with 1234, it’s quite a small number compared to what a 32 bit int can hold so its on the right side. Larger numbers would occupy further numbers towards the left.

Little endian numbers reverse the byte ordering so that the above example would be written as D2 04 00 00.

Its common for x86 architecture (PC) files and Intel Macs to be little endian and for PowerPC Macs and UNIX to use big endian. Particular file formats may choose to use little or big endian regardless of the architecture and operating system, however as a starting point I would assume the endianess matches the architecture.

In the case of Dune 2000 and most PC formats, files are stored in little endian. If you would like to read more about endianess try here.

Converting from decimal to a little endian 32 bit integer

1. Convert to hex using calculator
2. Prefix with ‘0’s until the number is represented as 4 bytes. (Has the structure 00 00 00 00).
3. Reverse the bytes, each grouping is a byte. So 12 34 56 AB becomes AB 56 34 12

Converting from a little endian 32 bit integer to decimal

1. Reverse the bytes, so AB 56 34 12 becomes 12 34 56 AB
2. Convert to decimal using calculator

Bit Representations in Bytes

A byte is made up of 8 bits. Each bit holds a 1 or 0 value, so a byte that holds the value zero can be represented as 00000000. The value that each digit represents doubles from right to left, starting at 1.

Adding across we have zero lots of each number, so a byte with the bit representation 00000000 = 0

If we take a byte who’s bits have a value of 11111111 and use the above grid, we get:

Adding across we get 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1

Which if we add it up, we find that a byte with a bit representation of 11111111 is 255 – the max value of a byte. The number of bits is the reason for the number of variations a number can hold. Try continuing the table across to represent 16 bits rather than 8 bits, add up all the top row numbers and compare against the integer data type table above.

Let’s take another example:

A byte with bit representation 00110010

Adding across again we get 32 + 16 + 2 = 50

Bit Fields

While the above usage of bits in a byte is the most common, it can be considered just one possible interpretation of the bits in the byte. Data only has meaning when we give it meaning. For example we could say rather than the right most bit representing the value 1, it could mean whether or not a tank can move onto a terrain tile. We could then say that the second to right byte which represents the value 2 can mean whether a player can build structures on this terrain tile. This usage of the bits in a byte is called a bit field. While bit fields are decreasing in usage now that data limits are getting higher and higher, they still have importance in many areas where small data sizes are critical.

Sub-byte data types

On a related note, you may want to hold more data than a simple true/false but want to use less data than a full byte. If say your maximum value was 15, then you’d only need 4 bits. You could then hold two different 4 bit variables in a single byte, one after the other. Alternatively, if you needed to hold a number with a ranger larger than a byte but smaller than 2 bytes, say a 12 bit number and you also wanted to hold a 4 bit number, you could combine the two by making use of 2 bytes. The first number occupying the first byte and the first half of the second byte, while the second number occupies the second half of the second byte. The below table shows the first number in red and the second number in green.

What’s next?

This post has been quite heavy in theory, in the next post I will explore data types through practical examples. So if you felt this was a lot to take in, don’t worry there will be opportunity to practice what I’ve talked about here and hopefully make sure you get your head around it.